Syntax and Semantics
The description of ontologies and knowledge in description logics uses constructs that have semantics given in predicate logic. However, due to historical reasons, different notation is used, that is closer to semantic networks and frame based systems. Let us have a look at the AL (attribute language) logic that is a minimal logic with a practically usable vocabulary. In the table below there is the syntax and semantics of the AL logic including a short comment. In the table as well as in the following description A and B are atomic concepts, C and D are concept descriptions, and R is atomic role. The semantics is defined using interpretation I that consists of non-empty set ΔI (the domain of interpretation) and an interpretation function, which assigns a set AI⊆ΔI to every atomic concept A and that assigns a binary relation RI⊆ΔI×ΔI to every atomic role R. The interpretation function is then extended by inductive definitions summarized in the table below. Two concepts C and D are equivalent, written C≡D, if CI=DI for all interpretations I.
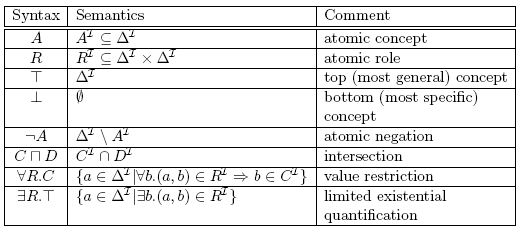
AL (attributive language) logic syntax and semantics
Let us illustrate the syntax and expressivity on a simple example. Let us suppose that Person and Female are atomic concepts. Then Person⊓Female is an AL concept describing persons that are female, i.e., women. In a similar way, Person⊓¬Female would describe man. In addition, let us suppose that hasChild is an atomic role. Then Person⊓∃hasChild.⊤ describes persons that have a child, and Person⊓∀hasChild.Female describes persons all of whose children are female.
Examples of AL logic basic extensions
The AL logic can be further extended by adding new constructs, see table above for examples. The name of the logic is then formed from the string AL[U][E][N][C], so for example the logic ALEN is the attributive language logic extended with full existential quantification and number restrictions. Some of the combinations are not unique from the semantic point of view - for example, union and existential quantification can be expressed using negation. Letter C is preferred to combination UE in logic name.
Some further extensions of ALC logic that will be of interest for us are as follows.
- S - role transitivity Trans(R) (asserting that role is transitive)
- H - role hierarchy R⊆ S (asserting hierarchy of roles)
- I - role inverse R- (creating inverse role)
- F - functionality
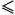 1 R (functional role in concept creation)
1 R (functional role in concept creation) - O - nominals {a1, ..., an} (concept declared by enumeration)
These constructors or axioms all extend the ALC logic and so it is enough to specify the extensions in the logic name - for example, logics SHIF and SHOIN will be interesting for us later in this introduction.
(c) Marek Obitko, 2007 - Terms of use
